Modeling the Rubik's Cube with OpenGL
Articles —> Modeling the Rubik's Cube with OpenGL
In a previous article, I set up a way to computationally represent a Rubik's Cube in Java where each cell - or color - is represented by both its color and three dimensional location. The model enables moves of the Rubik's Cube by rotating the appropriate cells within the 'pivot' around the appropriate axis, resulting in the mixing and matching of the colors of the changed sides. Below, I discuss how this model of the Rubik's Cube can be visualized.
One can render a Rubik's Cube in 2 and/or 3 dimensions. In two dimensions, the cube must be flattened such that the sides of the cube spread into the available space. In this case I used a custom painting algorithm within a java Swing JPanel, where I arbitrarily chose the location of each side: top, front, bottom, and back are drawn vertically down the middle in that order, while the left and right sides are drawn to the left and right (respectfully) of the front JPanel. The cells of each face in the model are found based upon their position and surface normal; for instance all cells on the front face have a location and surface normal with z=1. Once the cells are found it is only a matter of drawing them in the appropriate location:
private static final int PAINT_BORDER = 10; private static final int CUBE_SIZE = 20; ... /** * Converts the parameter to a color. * @param val The int constant of a Rubik's Cube cell color * @return A Color object. * @throws IllegalArgumentException if val does not represent a color */ private Color convertToColor(int val) throws IllegalArgumentException{ Color c = Color.black; switch ( val ){ case Cell.WHITE: c = Color.white; break; case Cell.GREEN: c = Color.green; break; case Cell.ORANGE: c = Color.orange; break; case Cell.BLUE: c = Color.blue; break; case Cell.RED: c = Color.red; break; case Cell.YELLOW: c = Color.yellow; break; default: throw new IllegalArgumentException("Invalid color type"); } return c; } .... Cell[] cube = new Cell[54]; ... //front java.util.List<Cell> selected = new ArrayList<Cell>(); for ( Cell n : cube ){ if ( n.getLocation().z == 1 && n.getNormal().z == 1 ){ selected.add(n); } } assert selected.size() == 9 : "Incorrect nodes on front face: " + selected.size(); //position the front in the second row, second column int xCenter = 5 * PAINT_BORDER + 4*CUBE_SIZE; int yCenter = 5 * PAINT_BORDER + 4*CUBE_SIZE; for ( int i = 0; i < 9; i++ ){ g.setColor(convertToColor(selected.get(i).getColor())); int xPos = xCenter + (CUBE_SIZE + PAINT_BORDER) * (int)selected.get(i).getLocation().x; int yPos = yCenter + (CUBE_SIZE + PAINT_BORDER) * (int)selected.get(i).getLocation().y; g.fillRect(xPos, yPos, CUBE_SIZE, CUBE_SIZE); }
For brevity, only snippets of the entire class is shown (delimited by an ellipsis), drawing only the front side of the Rubik's Cube. At this point, for those unfamiliar with the Rubik's cube model being used I recommend visiting my previous article on how to computationally represent the Rubik's Cube. The convertToColor method maps the int value representing color to a true java.awt.Color object we can use for rendering, and the cells of the Rubik's Cube are contained within an array of Cube objects. The results are shown below, in which 3 moves were made (shown in progression clockwise) - one of which is a full cube rotation - from the solved Rubik's Cube (upper left):
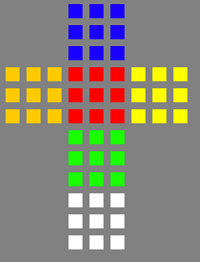 |
 |
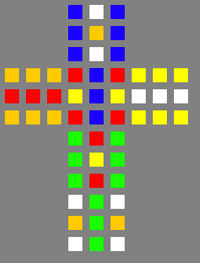 |
 |
Visualizing in 2-dimension is a nice way to validate any rotation algorithms, visualize the general status of the Rubik's cube, or as a way which allows users to input values for an unsolved Rubik's Cube. However, a Rubik's cube is 3-dimensional, and what better way to visualize the cube than to do so in using all dimensions. Although one can use their own favorite 3D rendering engine, I chose JOGL OpenGL bindings to draw the cube. Each cell was rendered by generating vertices around the cell's x,y,z location, the generation of these vertices done by offsetting the cell location in directions perpendicular to the face axis (or cell surface normal). I chose +/- 0.49 as an offset from the cell center (recall x,y,z values of -1,0, and 1 were arbitrarily chosen to restrict cell location). Offsetting the cell location in all four plausible direction leads to four vertices of a quadrangle. For example, consider the upper left cell of the front face (x = -1, y = 1, z = 1): the axis perpendicular to the face is the z axis (its surface normal is (0,0,1)) - thus we modify its x and y values, resulting in the following vertices:
| Vertex | X | Y | Z |
| 1 | -1.49 | 1.49 | 1 |
| 2 | -0.51 | 1.49 | 1 |
| 3 | -0.51 | 0.51 | 1 |
| 4 | -1.49 | 0.51 | 1 |
The spacer of 0.49 was chosen as it leaves a small amount of space between the quadrangles (Rubik's Cube cells), and these spaces become background color with the appropriate rendering, creating the seams of the Rubik's Cube. Below is a snippet of code demonstrating the drawing method used, which draws a cell on the front face of the Rubik's cube using JOGL and OpenGL:
Cell[] cube = new Cell[56];
...
gl2.glBegin( GL2.GL_QUADS );
gl2.glNormal3d(cells[i].getNormal().x, cells[i].getNormal().y, cells[i].getNormal().z);
gl2.glVertex3d(cells[i].getLocation().x - SPACER, cells[i].getLocation().y + SPACER, cells[i].getLocation().z + SPACER);
gl2.glVertex3d(cells[i].getLocation().x - SPACER, cells[i].getLocation().y - SPACER, cells[i].getLocation().z + SPACER);
gl2.glVertex3d(cells[i].getLocation().x + SPACER, cells[i].getLocation().y - SPACER, cells[i].getLocation().z + SPACER);
gl2.glVertex3d(cells[i].getLocation().x + SPACER, cells[i].getLocation().y + SPACER, cells[i].getLocation().z + SPACER);
gl2.glEnd();
Although I am omitting the full length of code here for brevity*, the video below - created from screenshots and assembled using ffmpeg - shows the results. In this video, the code solves a leniently scrambled Rubik's Cube. Each move was animated by rotating the appropriate cells by a small angle until the move is complete.
*Code available upon request
Comments
- Rodrigo Siqueira - October, 3, 2014
Hi, I'm currently studying OpenGL in my university, is it possible for you to send me the code so i can study it? Thanks in advance :)
- James Holman - February, 8, 2016
I would like the code as well. I am trying to make an app for android that is both a timer and a simulator. I got the timer part, but I need the code you have in the simulator. I noticed there were ellipses. Can you also send what belongs there? Thanks!
James Holman
- Philip Dam - May, 10, 2016
Thank you for a very nice article. I have tried to make the implementation of the rotation without luck, so I would very much like to have the opportunity of analysing the code, if you will be so nice to grant me access to it.
- Raj Singha - August, 13, 2016
It is a really nice article. I am doing a project work based on java opengl . I will be glad if you give me the code so that i could clear java opengl concept. It will help me a lot.
- Tina Zhang - October, 1, 2016
Could you please share the code? I would like to take a look and learn it. Thank you in advance.
- Burak Uzunboy - March, 21, 2017
Hi, I'm working on computer graphics and I need similar things for my assignment. Can you send me the codes? Thanks for your advance.
- Lucas Saccumann - June, 22, 2017
Hi, i'm currently studying openGL and it would be very nice if you could send me the code, i found the rubik's cube project very interesting. Thanks in advance!
- j P - March, 22, 2018
Hi, I'm currently studying OpenGL in my university, is it possible for you to send me the code so i can study it? Thanks in advance
- Felix Nyman - August, 21, 2019
I'm trying to make a Rubik's cube solver but don't know where to start. it would be great if you'd be so kind to share your code with me. Thanks in advance.
- Josue Cano - April, 15, 2022
Buen dia podría proporcionarme el código del cubo en opengl java, ya que tengo problemas a la hora de mover las piezas
- Ahmad Sliman - December, 5, 2022
Hi, I\'m currently studying OpenGL in my university, could you send me the code so i can study it? \r\nThanks