Optical Character Recognition using PCA
Articles —> Optical Character Recognition using PCA

Optical Character Recognition (OCR) is a complex classification task in the field of computer vision in which images of text are analyzed for their content - in essence translating text within images into the text itself. This can be useful in a wide range of fields, from reading text from scanned documents to mail sorting. OCR can be implemented on a range of data - from clean (type written) to noisy (handwriting) - the input of which can make OCR relatively easy to extremely difficult and error prone. Either way the implementation of optical character recognition is not trivial, and there are many different ways in which OCR can be implemented, from using neural networks to scale invariant feature transform (or SIFT).
The method discussed below implements OCR for character classification by using statistics and linear algebra to create the equivalent of what are called eigenfaces. Eigenfaces get their name from facial recognition in which the statistical analysis of a collection of images depicting the faces of people abstracts out the fundamental features of the faces. To create eigenfaces, a method called Principle Component Analysis (PCA) is used. This method creates vectors - called eigenvectors - representative of the general features of the images.
Here I apply the same technique to character recognition. As with any supervised machine learning technique, one must first have a training set to train the model. Below I outline how this is achieved, how the training set is used to fit the model, how the model makes predictions, and finally some analysis of the accuracy of this method.
The Training set
In this example I created several images consisting each of a number or letter of the alphabet (both upper and lower case). To create these images I used the following java code:
public static BufferedImage getImageForString(String a, Font font){ BufferedImage image = new BufferedImage(width,height,BufferedImage.TYPE_BYTE_GRAY); Graphics2D g = (Graphics2D)image.createGraphics(); g.setColor(Color.white); g.fillRect(0,0,width, height); g.setColor(Color.black); g.setFont(font.deriveFont((float)width)); g.drawString(a, 5, height-5); g.dispose(); return image; }
The method above returns an image of the parameter character (defined as a String) in the specified Font, where width and height were defined as 30. Looping over several Fonts and the alphabet yielded hundreds of images to be used as training.
For the following analysis, a mean image must be generated representing the mean pixel value of all images. To do so the mean value of each pixel was calculated for each pixel location - for instance pixel 0,0 is the average of the pixel value of 0,0 from all images.
Principal Component Analysis
To perform PCA on the images a covariance matrix must be generated. To do so a matrix M was created in which each column represents an image, and each row a pixel of said image. Here the columns are the linear representation of the 2D pixel data - I organized the images linearly as one reads image pixel values from left to right and top to bottom. The values were then mean centered by subtracting the corresponding pixel value of the mean image.
Next, a covariance matrix was generated from the matrix M created above. The covariance matrix is defined as (x - x')*(y - y'), and can be represented formally as C = M*MT. The covariance matrix C is then used to compute the matrix eigenvectors. Eigenvectors and their calculation is beyond the scope of this article, suffice it to say many tools exist to allow one to calculate the eigenvectors of a matrix. In this case I relied on the Apache Commons Math package, in particular the EigenDecompositionImpl class to generate the eigenvectors.
The 'eigenfaces' - here called 'eigencharacters' - can be generated to visually depict the eigenvectors. To do so, the values of each eigenvector was normalized to pixel values (0-255): value = 255 * (eigenvector[n] - min) / (max - min) and mapped back to a 2d image:

First thirty 'eigencharacters' generated from principle component analysis of images of characters.
Image Weighting
Each eigenvector can be thought of as representing a particular feature of the letters and numbers as a whole, and each eigenvector contributes a certain value towards each image - here defined as the weight or score. The weight of an eigenvector for an image can be calculated by calculating the dot product (the sum of the product of each index value - eigenvectorn and pixeln) of the eigevector and the mean centered pixel values of the character image (in column form M).
Prediction
The class of a new 'unseen' test image can be predicted by first calculating its weight as described above. The prediction can then be generated by calculating the distance of the eigevector weights of the test image relative to those in the training set. To calculate the distance one can use Euclidian distance, a method which generates a numeric value representing how close or distant the objects are given the input parameters (here the weights) - the smaller the distance the better.
Results
The algorithm above was implemented in java and ran through a series of test. First was the simple proof-of concept (POC). All letters (lower case and upper case) were generated as images in four different font faces. Then, the prediction accuracy of all lower case letters in one font was tested. The results were surprising: 100% accuracy - every letter correctly classified.
Of course, the above POC was making predictions on data already seen in the training. How robust is this method in making predictions for data not seen in the training? Using the same technique as above, I left out a random 30%, trained on the remaining 70%, then tested the model for accuracy on the 30% left out. This led to an accuracy of ~70%.
Letters and numbers are fairly consistent elements, thus the leave data out may not be the best evaluation of accuracy. More important may be transformations and noise - how does the model do in predicting rotated, translated, or noisy images of characters? To address this question I trained on all characters (10 Fonts) and tested permutations of the training set. Below is a chart showing the accuracy of prediction of all lower case letters relative to the angle of rotation.
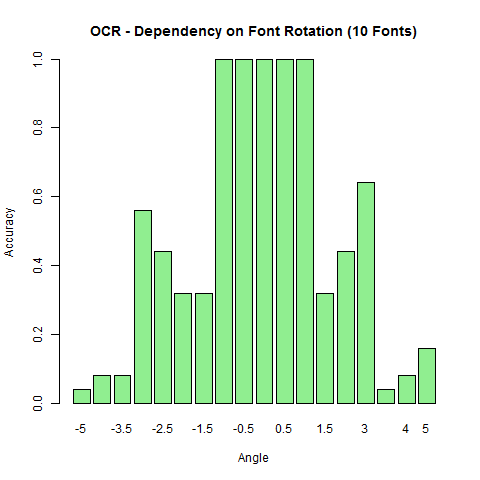
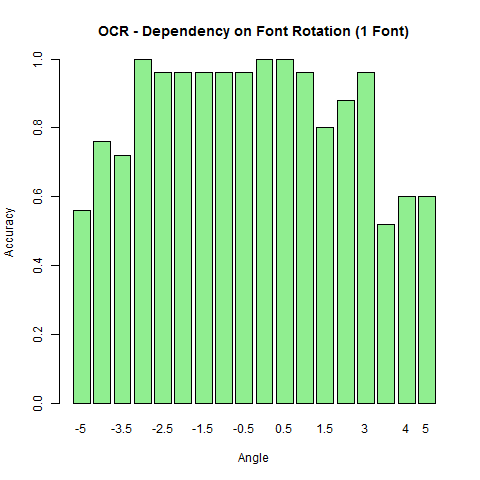
Beyond an angle of 1 degree the model begins to break down. Interestingly, the story is different if the model is trained on a single font (times) - the rotation is more tolerable of rotation.
Conclusion
While feasible in this controlled context, the above method can be susceptible to great many issues such as noise, rotation, and scale. Further, this is not extremely efficient - each test requires analysis against every letter. Additional wrappers of learning or heuristics can be applied to speed up the process. Lastly, one needs a method to extract each character from an image in order to perform the analysis on individual characters - a large task in and of itself.
Comments
- Omkar Lad - October, 29, 2014
PCA is not a supervised learning algorithm. Supervised algorithms tell the system about class of objects, while PCA doesn't. Good article though! Kudos
- Greg Cope - October, 30, 2014
Thanks for the information Omkar Lad!
- Jack Simpson - June, 9, 2015
If I trained my data with letters of varying angles and illumination could that work or would I be better off using Fisherfaces for this task?